II. Géodésie
II.2 Des coordonnées, oui mais dans quel système ?
- Systèmes de coordonnées
- Coordonnées en deux dimensions : les projections
- A retenir
- Quelques ressources internet
Les coordonnées peuvent être exprimées en degrés, en mètres... et dans des référentiels différents. Un même point aura des coordonnées différentes selon le système de coordonnées utilisé.
Systèmes de coordonnées
Qu'est-ce qu'un système de coordonnées ?
Un système de coordonnées est un système utilisé pour mesurer des coordonnées. Il peut être défini par un ellipsoïde. Un point sera alors localisé par ses coordonnées géographiques, exprimées par la latitude Ф, la longitude λ, et la hauteur ellipsoïdale h mesurée suivant la normale à l'ellipsoïde.
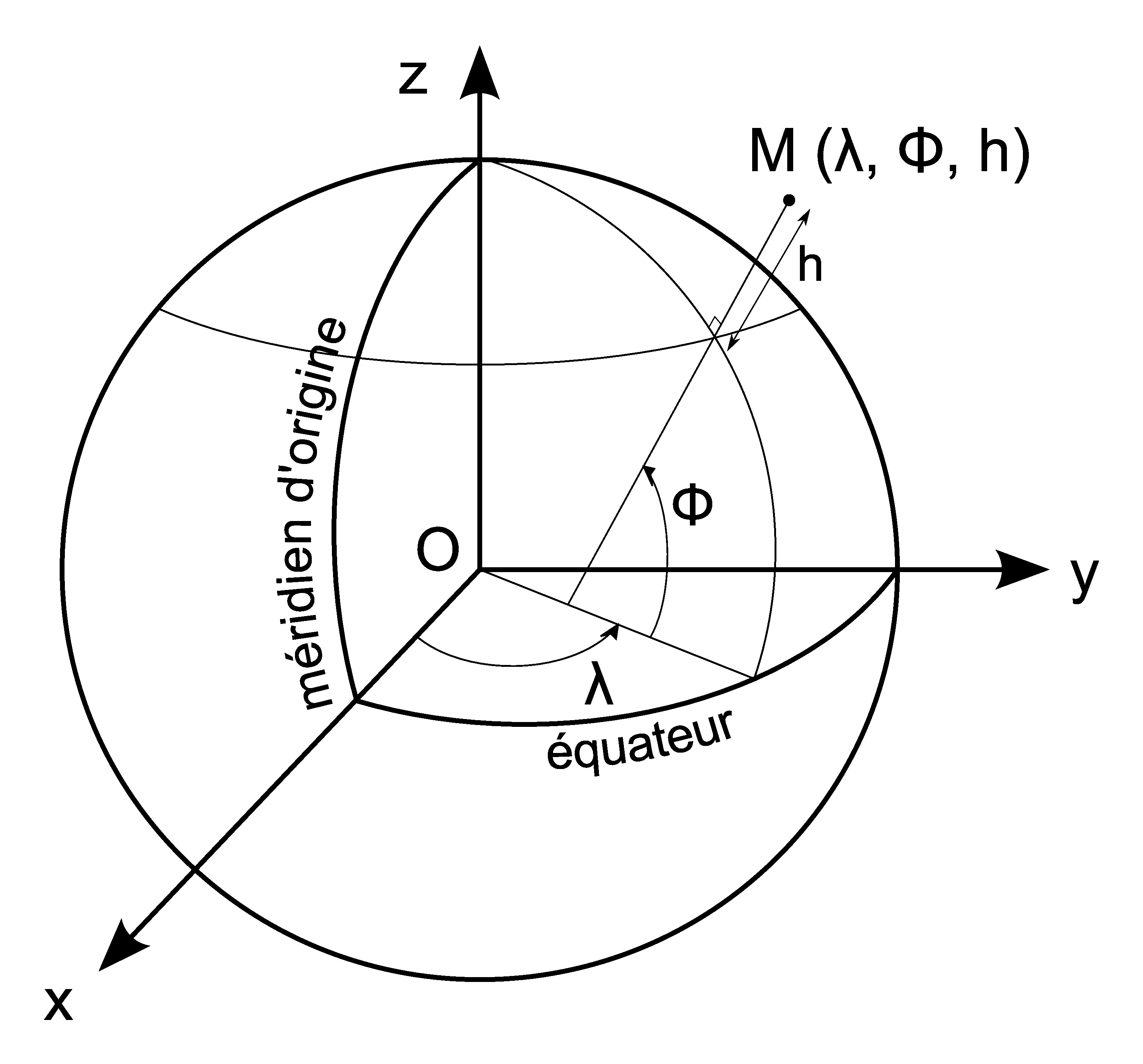
Longitude et latitude sont des mesures d'angles et peuvent être exprimées en degrés, en grades ou en radians.
Attention à ne pas confondre la hauteur ellipsoïdale, mesurée par rapport à l'ellipsoïde, et l'altitude normale mesurée par rapport au géoïde. Avant les années 1960, les altitudes étaient mesurées par rapport au niveau de la mer (altitude orthométrique).
Quelques exemples de systèmes de coordonnées
Il existe de nombreux systèmes de coordonnées. Ils sont recensés par l'EPSG (European Petroleum Survey Group) qui a attribué un code à chacun. Quelques exemples :
WGS84 (World Geodetic System 1984) :
Système global initialement mis au point par le département de la défense des États Unis en 1984, mis à jour en 2004. Son exactitude est métrique, et son ellipsoïde se nomme IAG-GRS80.
RGF93 (Réseau Géodésique Français 1993) :
Système global obtenu par densification des points du réseau mondial associé ETRS89. Il s'agit du système officiel français. Ce système est facilement compatible avec le WGS84 par exemple.
ED50 (European Datum 1950) :
Système européen mis en place à la suite de la seconde guerre mondiale. Son ellipsoïde associé se nomme Hayford 1909.
NTF (Nouvelle Triangulation de la France) :
Système local issu de mesures réalisées depuis la fin du XIXème jusqu'en 1991. Son ellipsoïde associé est Clarke 1880 et son méridien d'origine Paris.
En France, le système NTF a été abandonné au profit du système RGF93 qui présente une meilleure compatibilité avec les autres systèmes mondiaux. Il existe toutefois encore aujourd'hui de nombreuses données utilisant le système NTF.
Certains systèmes seront adaptés à une zone précise, d'autre à la Terre entière. Plusieurs systèmes coexistent souvent pour une même zone, en raison par exemple de l'avancée des techniques ou de règlements.
Un même point aura des coordonnées différentes selon le système utilisé pour les mesurer. Le tableau ci-dessous montre les coordonnées de Paris dans différents systèmes.
| Système de coordonnées | Code | Latitude (en degrés) | Longitude (en degrés) |
|---|---|---|---|
| WGS84 | EPSG:4326 | 48,856700 | 2,351000 |
| ED50 | EPSG:4230 | 48,857615 | 2,352286 |
| RGF93 | EPSG:4171 | 48,856700 | 2,351000 |
| NTF | EPSG:4807 | 48,856769 | 0,014494 |
On sait maintenant comment un point peut être défini par 3 coordonnées X, Y et Z. Comment représenter maintenant la Terre en 2 dimensions, pour en faire une carte par exemple ?
Coordonnées en deux dimensions : les projections
Qu'est-ce qu'une projection ?
Le principe est de projeter des données 3D sur une surface plane. Il y aura donc forcément des déformations : pensez à une peau d'orange qu'on écrase, et qui va se déchirer.
On appelle projection cartographique le système de correspondance entre les coordonnées géographiques (donc mesurées avec un système de référence) et les points du plan de projection.
De nombreuses méthodes de projections existent, chacune adaptée à un usage différent.
Lorsqu'on utilise une projection, on parle de coordonnées projetées. Ces coordonnées sont par définition bidimensionnelles, et seront exprimées généralement en unités métriques.
Une projection permet donc de représenter sur une surface plane une partie d'un modèle ellipsoïdal, mais aussi :
- d'obtenir des valeurs métriques plus facilement exploitables que les valeurs angulaires de latitude et longitude
- de rendre plus facile une évaluation des distances
Trois grands types de projections : cylindriques, coniques et azimutales
Dans tous les cas, on va projeter la surface de la Terre sur une forme que l'on peut dérouler pour obtenir une surface plane : un cylindre, un cône ou un plan. On distingue ainsi les projections cylindriques, coniques et azimutales. Il existe d'autres types de projections.


A chaque projection ses déformations
On peut aussi classer les projections selon leurs propriétés. On distingue ainsi :
- les projections équivalentes qui conservent les surfaces
- les projections conformes qui conservent les angles.
- les projections aphylactiques, ni conformes ni équivalentes. Elles peuvent être équidistantes, c'est-à-dire conserver les distances sur les méridiens.
Une projection ne peut être à la fois conforme et équivalente.
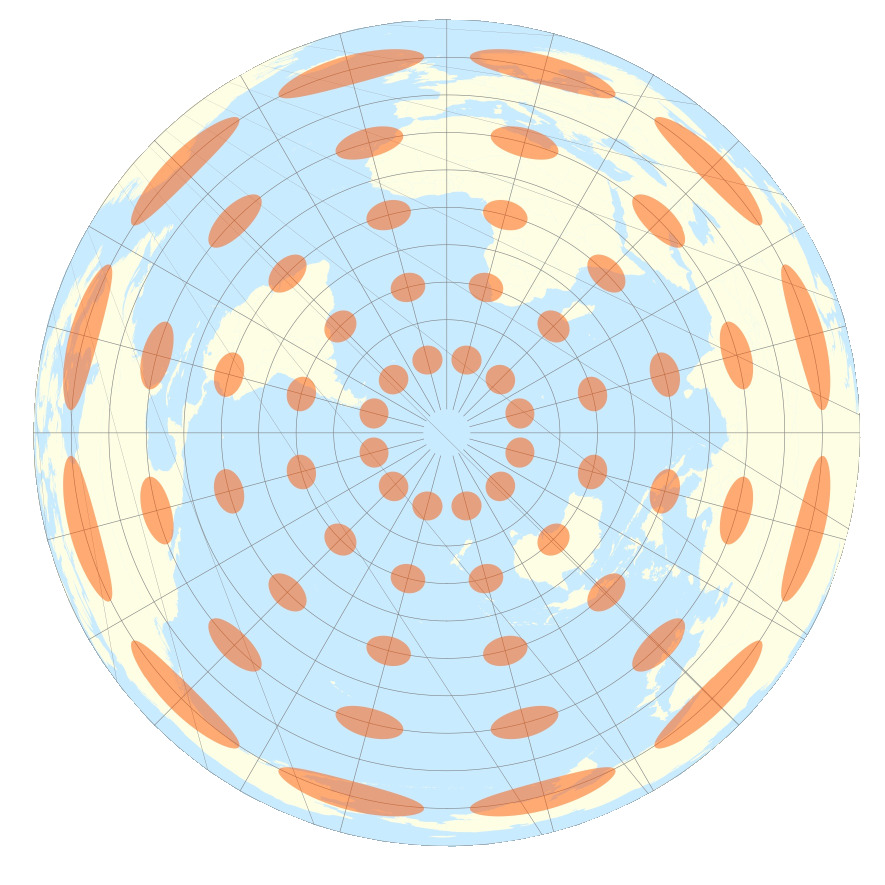
Pour visualiser les déformations liées à une projection, on peut utiliser les indicatrices de Tissot. Ce sont des cercles identiques dessinés sur la Terre avant projection, qui se retrouveront donc déformés après projection. Si la projection déforme les angles, les cercles seront transformés en ellipses, si elle déforme les surfaces les cercles auront des surfaces différentes.
Quelques exemples de projections
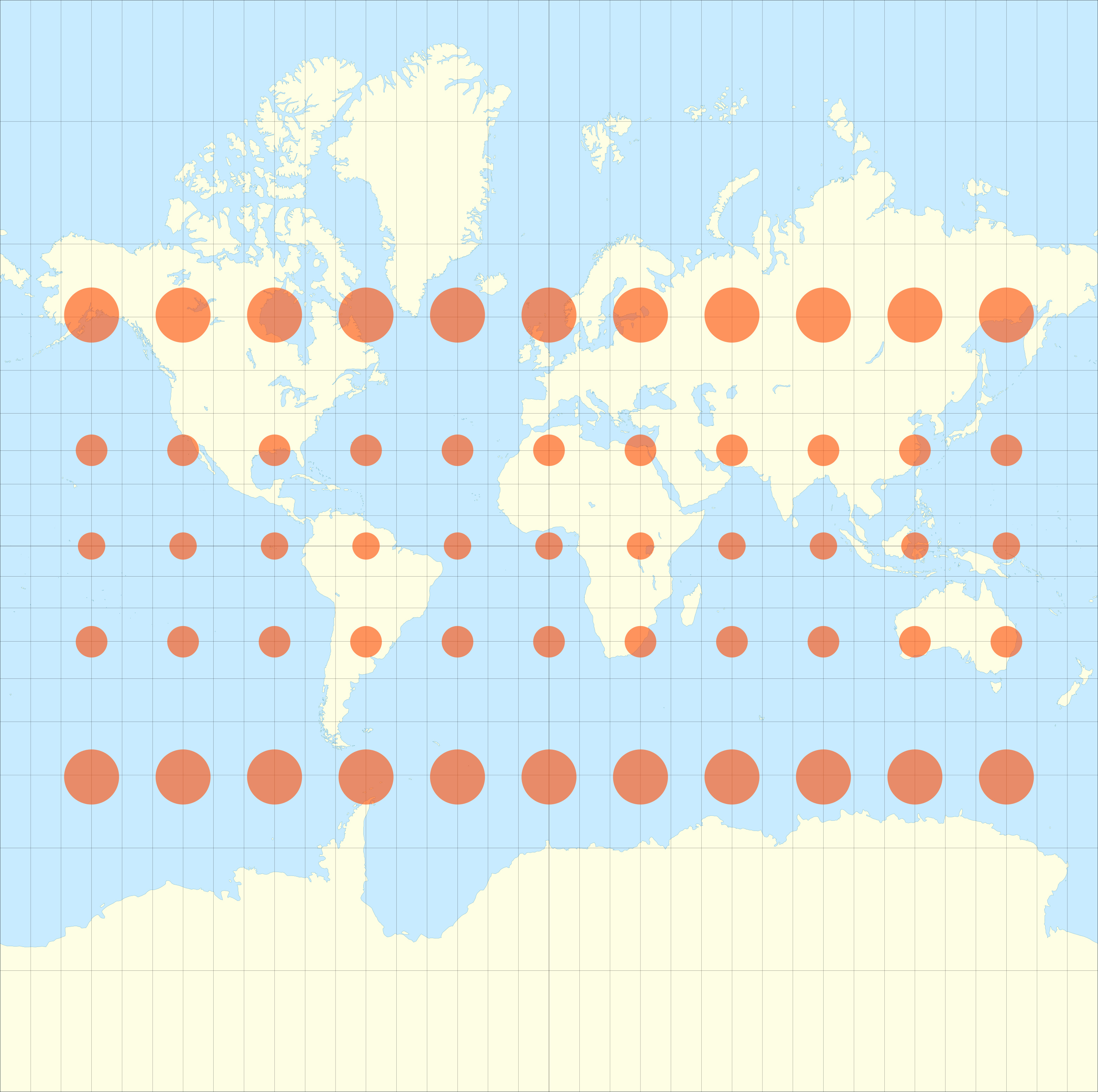
Projection cylindrique conforme de Mercator
Cette projection conserve les angles, mais déforme de plus en plus les surfaces au fur et à mesure qu'on se rapproche des pôles. Elle est largement utilisée, notamment par Google.
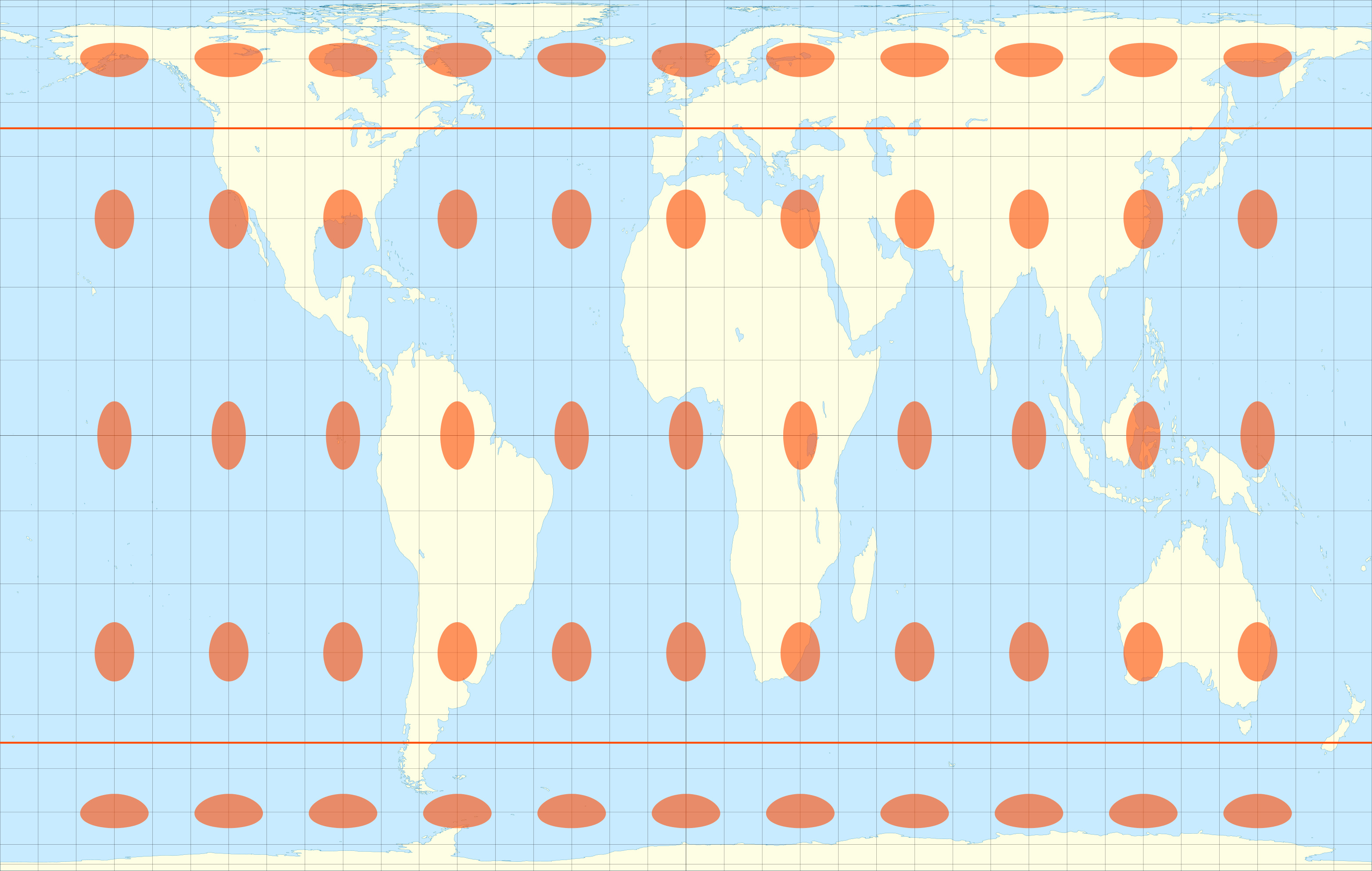
Projection cylindrique équivalente de Peters
Cette projection permet une vision juste des proportions des surfaces des continents, mais ne garde pas les bonnes formes au contraire de la carte de Mercator. Elle permet notamment d'éviter de sous-dimensionner les pays du Sud.
Projection conique conforme de Lambert
Contrairement aux projection de Mercator et Peters, cette projection est utilisée pour représenter seulement une partie du globe. Suivant ses paramètres, la zone couverte sera différente. L'illustration montre la projection Lambert 93, projection officielle française : les déformations sont minimisées pour la France.
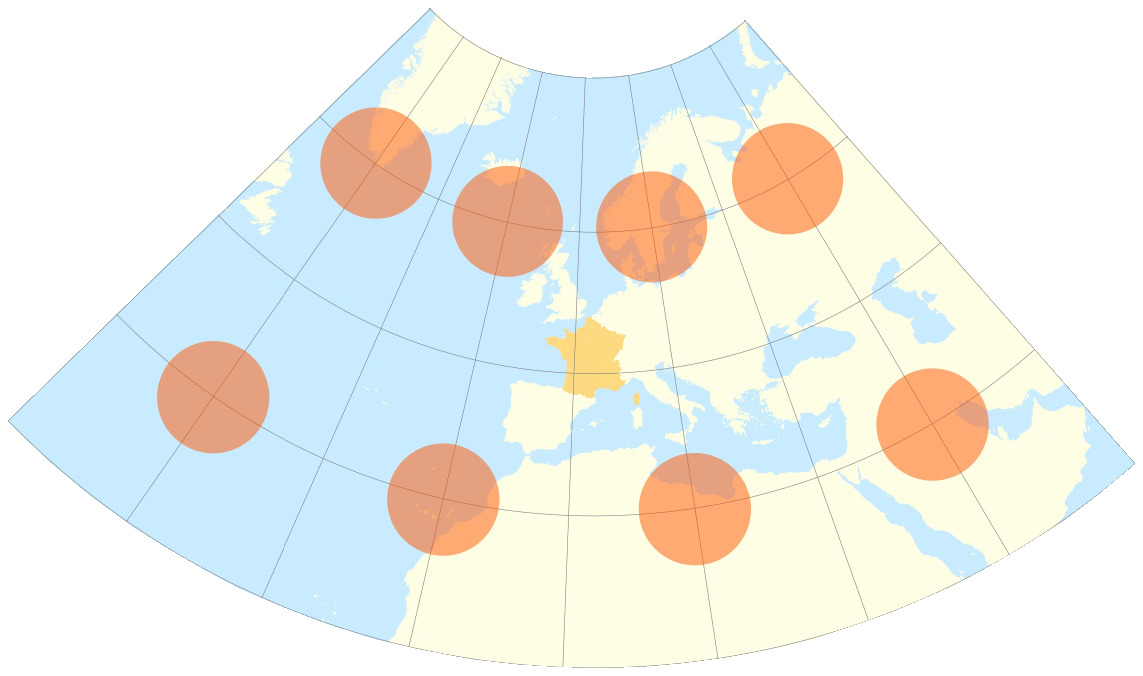
Projection azimutale équidistante du pôle sud
Projection Transverse Universelle de Mercator (UTM)
Il s'agit en fait d'une série de projections, le monde étant divisé en 60 fuseaux de 6° de longitude. Une projection différente est utilisée pour chaque fuseau : le cylindre utilisé subit à chaque fois une rotation légèrement différente. Ceci permet de minimiser les déformations. La France est ainsi traversée par 3 fuseaux : 30, 31 et 32. Cette projection peut être associée au système WGS84, ou ED50 par exemple.
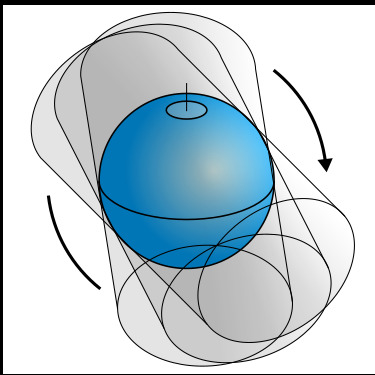
Par Javiersanp (Travail personnel) [CC-BY-SA-3.0 ou GFDL], via Wikimedia Commons
Un même point aura des coordonnées différentes selon la projection utilisée (et le système associé à cette projection). Ci-dessous, les coordonnées de Paris mesurées dans différents sytèmes et projections.
| Système et projection | Code | X (en mètres) | Y (en mètres) |
|---|---|---|---|
| Mercator | EPSG:54004 | 261712 | 6218386 |
| Peters | SR-ORG:22 | 185369 | 6753027 |
| RGF93 Lambert93 | EPSG:2154 | 652381 | 6862047 |
| Azimutale équidistante pôle sud | EPSG:102019 | 632368 | 15402681 |
Il existe d'autres types de projections, ni cylindriques, conformes ou azimutales.
En résumé, la projection parfaite n'existe pas ; il faut essayer de faire au mieux pour l'usage auquel on destine la carte (à ce sujet, vous pouvez voir ce film). Par exemple, les cartes utilisées pour la navigation conservent généralement les angles et non les distances. L'échelle de la carte influe également sur le choix de la projection.
A retenir
On peut exprimer les coordonnées d'un point :
- sous forme de coordonnées géographiques en degrés : latitude, longitude, hauteur ellipsoïdale. Ces coordonnées sont calculées dans un système géodésique de référence, sans utilisation de projection
- sous forme de coordonnées en projection en mètres (représentation plane), calculées dans un système géodésique de référence et avec une projection cartographique
Exemple : les coordonnées de Paris peuvent être exprimées sous forme de coordonnées géographiques en degrés dans le système RGF93, ou bien sous forme de coordonnées projetées en mètres dans le même système RGF93 avec en plus utilisation de la projection Lambert 93.
Il est à noter que la projection Lambert 93 a été conçue pour être utilisée uniquement avec le système RGF93.
Chaque ensemble système de coordonnées et projection s'il y en a une, ou simplement système de coordonnées, est référencé par un code, généralement défini par l'EPSG.
Pour simplifier, dans le reste de ce tutoriel, le système de coordonnées et sa projection associée s'il y en a une seront nommés SCR (Système de Coordonnées de Référence) suivant la terminologie utilisée par QGIS.
Quelques ressources internet
- Comprendre le principe des projections : la carte impossible
- « Déplier la Terre » pour mieux comprendre certaines projections : Myriahedral Projections
- Visualiser les déformations liées à des projections : Surface Area of a Sphere
- Liste des systèmes de coordonnées avec leurs codes EPSG ou autre : http://spatialreference.org/
- Comparaison de projections : https://blocks.roadtolarissa.com/syntagmatic/ba569633d51ebec6ec6e et https://www.map-projections.net/imglist.php
- Aide au choix d'une projection : http://projectionwizard.org/
- Sur la précision des coordonnées : jusqu'où faut-il aller dans le nombre de décimales ? https://xkcd.com/2170/
chapitre précédent chapitre suivant
haut de page

